1. Documentation
2. 2025.0 (Latest) 2024.1 2024.0 10.3 10.2 10.1 10.0 9.10 9.9 9.8 9.7 9.6 9.5 9.4 9.3 9.2 9.1 9.0 8.2 8.1 8.0 7.6
3. Studio
4. Guided
5. Auto Model

Auto Model

Whether you're just starting out with Altair AI Studio, or you're an old hand, Auto Model can make your life easier. Auto Model is an extension to Altair AI Studio that accelerates the process of building and validating models. Best of all, it creates a process that you yourself can modify or put into production -- there are no black boxes!

Auto Model addresses three large classes of problems:

• Prediction
• Clustering
• Outliers

Within the Prediction category, you can solve both classification and regression problems. Auto Model helps you to evaluate your data, provides relevant models for the solution of your problem, and helps you to compare the results for these models, once the calculations are completed.

Auto Model not only helps you to get results; it also helps you to understand those results, even for models such as Deep Learning where the inner logic may be hard to understand. Within Altair AI Studio, Auto Model appears as a view, next to the Design view, the Results view, and Turbo Prep.

Example: Predict Survival on the Titanic

To show how Auto Model works, we'll use one of the data sets that is bundled with Altair AI Studio, the Titanic data set, and use it to predict survival on the Titanic. To get started, choose the Auto Model view by pressing the button at the top of Altair AI Studio.

Select Data

After starting Auto Model, the first step is to select a data set from one of your repositories. If your data isn't in a repository, click on the link at the top of the screen where it says "import new data first".

In our example, the Titanic data set can be found under Samples > data. Select this data set, and click on Next at the bottom of the screen.

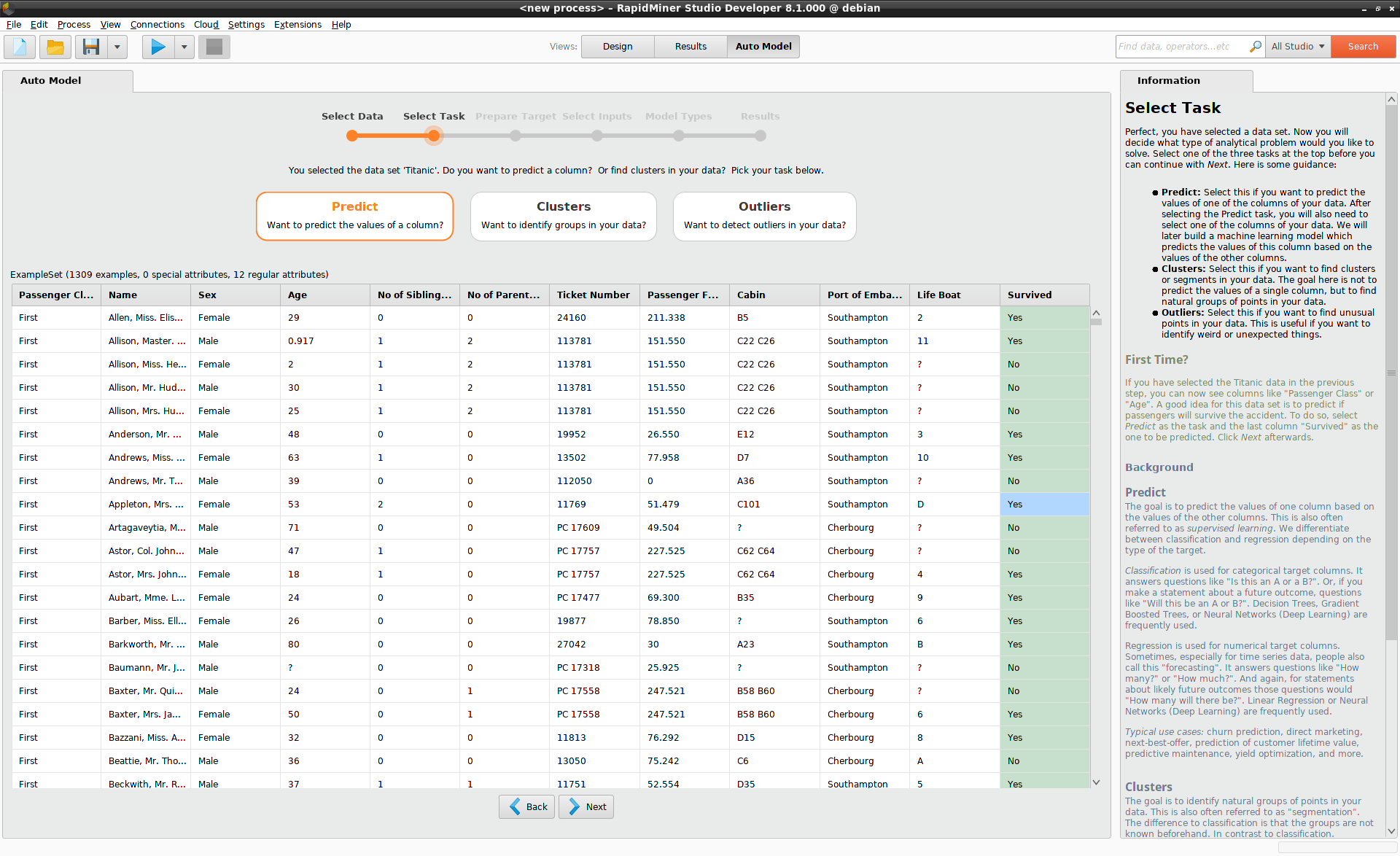
Select Task

Having selected a data set, you have to decide what kind of problem you want to solve. Auto Model identifies three different tasks:

• Predict
• Clusters
• Outliers

In our example, we want to predict survival on the Titanic, so you should select Predict, and click on the "Survived" column, before clicking Next.

Prepare Target

Since "Survived" has only two values, "Yes" or "No", the problem is a classification problem. In general, for classification problems, Auto Model will display a bar chart with the number of data points in each class. When there are more than ten classes, only the 10 classes with the most data points are displayed.

Class of Highest Interest

The Class of Highest Interest becomes important later, when the results are presented, because performance values such as "Precision" and "Recall" depend on knowing which of the classes should be interpreted as a "positive" result. In our example on the Titanic, the Class of Highest Interest is "Yes".

Map Classes to New Values

This step includes the option of renaming the target values from "Yes" and "No" to some other values. When there are more than two classes, this option may be more useful, because it can be used to combine classes. When entering a new value, be sure to finish by pressing the Enter key. In our example, we will ignore this option. Click Next to continue.

Select Inputs

Not all of your data columns will help you to make a prediction. By discarding some of the data columns you may speed up your model and / or improve its performance. But how do you make that decision? A key point is that you're looking for patterns. Without some variation in the data and some discernible patterns, the data is not likely to be useful.

A quick summary of things to look out for includes the following, whose values are displayed alongside the quality bars for each data column.

• Columns that too closely mirror the target column, or not at all (Correlation),
• Columns where nearly all values are different (ID-ness),
• Columns where nearly all values are identical (Stability),
• Columns with missing values (Missing).

Auto Model summarizes the situation with a color-coded status bubble (red / yellow / green). As a general rule, it is a good idea to deselect at least those columns that have a red status bubble, but of course you may deselect any columns you like, independent of their status. The input for the machine learning model will only include the selected columns.

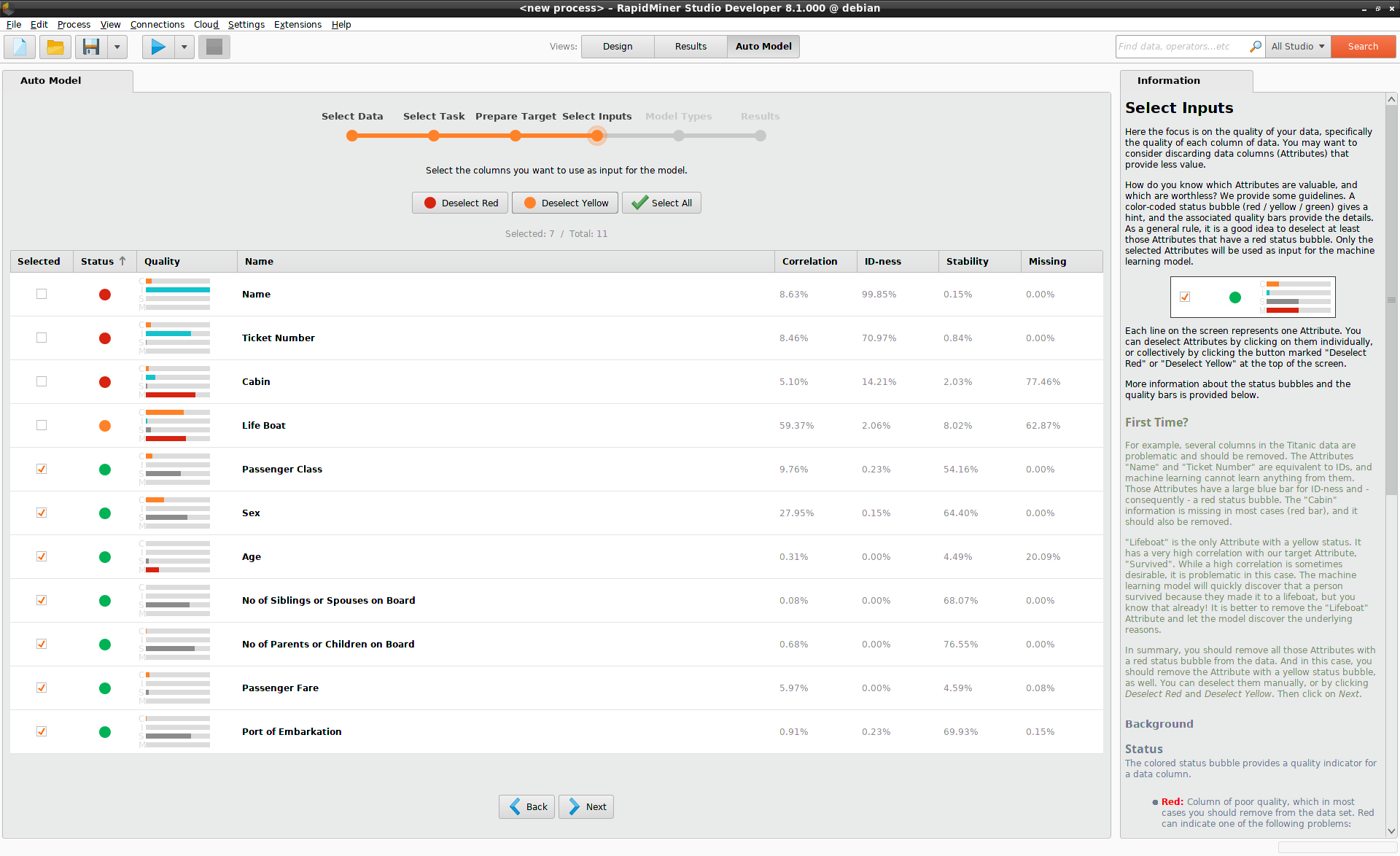
In the case of the Titanic, the "Name" and "Ticket Number" are equivalent to IDs. The "Cabin" values are missing for most passengers. Hence, these three columns, with a red status bubble, should be discarded when building a model. None of them is helpful in discovering a pattern.

"Life Boat" has a yellow status bubble, because the data in this column is highly correlated with "Survived". "Lifeboat" and "Survived" are effectively synonyms, so it is better to remove the data from the "Life boat" column and let the model discover the underlying reasons for survival.

Put somewhat differently, you expect the model to help you make a plan. A passenger can't know in advance whether he will be on a lifeboat, so that can't be part of the plan, but he can decide how much to pay for his ticket, and whether or not to bring his family along.

In this example, you should also deselect the data with the yellow status bubble, "Life Boat", and press Next.

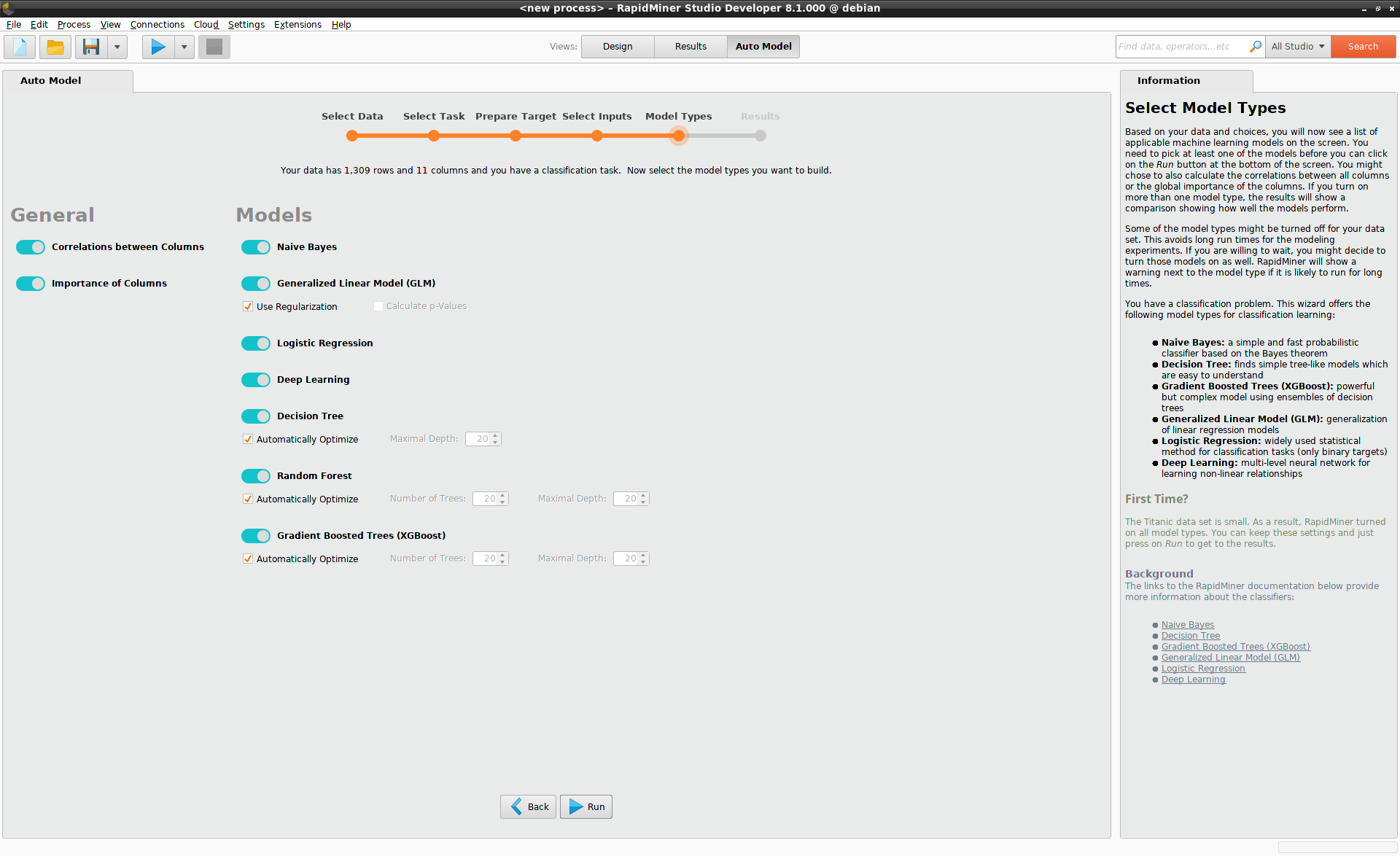
Model Types

Auto Model provides you with a selection of models that are relevant for your problem. If there is no time constraint, the best option is probably to build all of them, and compare their performance once they are finished. Typically, you have to decide on your priority: is it the accuracy of the finished model, or is it the time it takes to build it? Auto Model helps you to arrive at a reasonable compromise.

In the Titanic example, Auto Model provides the following models:

• Naive Bayes
• Generalized Linear Model
• Logistic Regression
• Deep Learning
• Decision Tree
• Random Forest
• Gradient Boosted Trees (XGBoost)

Press Run to build the models and generate the results.

Results

Depending on your data set and the models you selected, you may have to wait for the results. The progress bar at the top tracks the status of an ongoing calculation. You can stop model-building at any time by pressing the Stop button. Intermediate results are displayed as they become available, e.g., under Comparison > Overview.

In the case of the Titanic data set, the Gradient Boosted Trees (XGBoost) model takes the longest time to build, but it is also the most accurate model. See Comparison > Overview to compare the models' accuracy and runtimes. Given the marginal performance advantage of Gradient Boosted Trees over Deep Learning, and the considerably longer runtimes, you may prefer to use a Deep Learning model in this case.

The Model Simulator and Other Useful Operators

Auto Model not only helps you to get results; it also helps you to understand those results. Deep Learning is notorious for creating accurate but non-intuitive models; witness the model description displayed under Deep Learning > Model. In what follows, we will explore the Deep Learning model, using some helpful user interfaces provided by Auto Model.

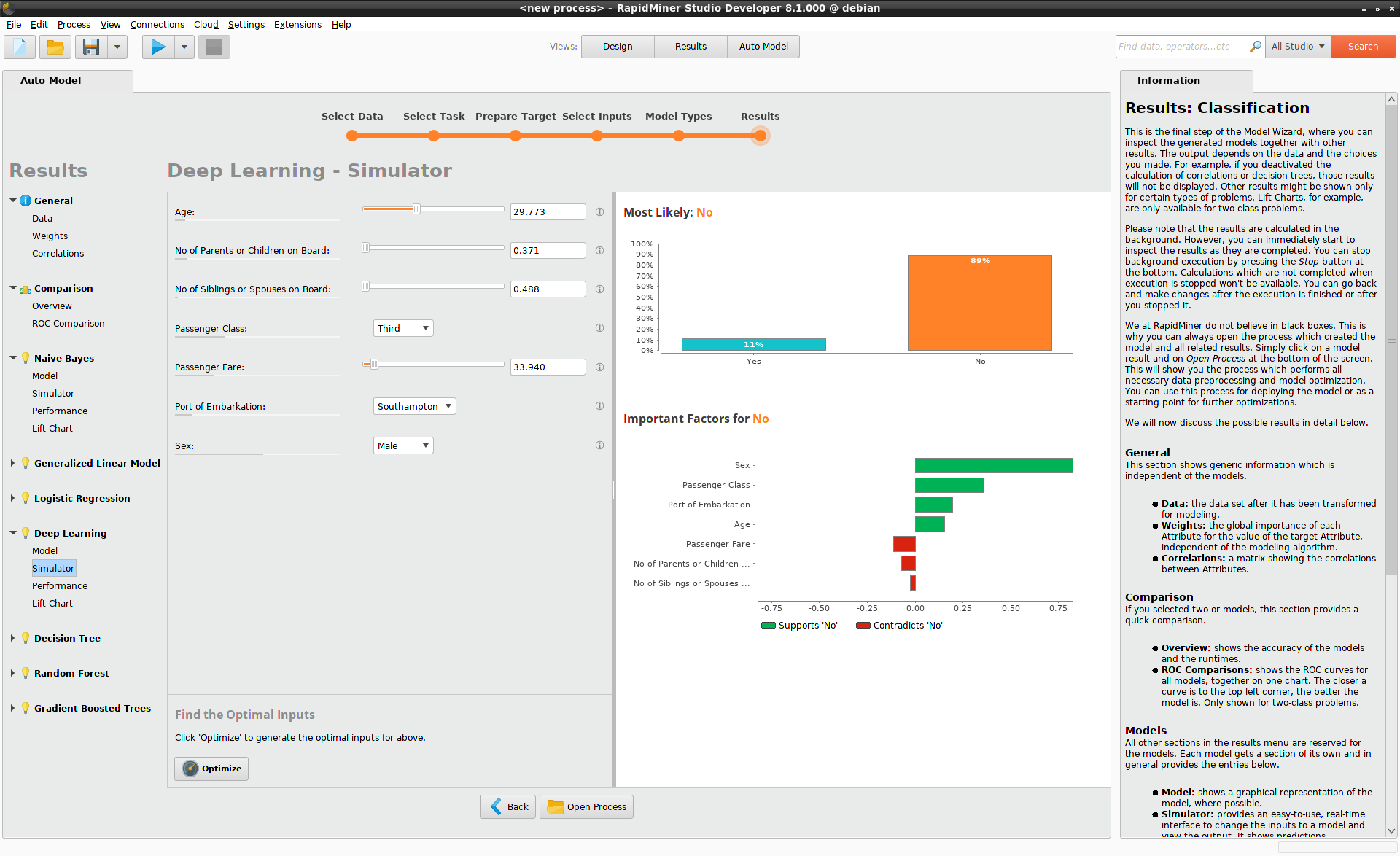
Model Simulator

To get a better insight, select Deep Learning > Simulator. Here you will see a user interface with sliders and dropdown lists on the left, and bar charts on the right. For its inital state, the Model Simulator chooses average data values. On the Titanic, this average corresponds to a third-class male passenger about 30 years of age, with relatively few relatives on board.

The most likely scenario, according to the upper bar chart on the right, is that this passenger will not survive. His probability of survival is 11%. The lower bar chart explains what is against him: above all, it is his Sex and his Passenger Class, displayed as green bars. Green in this context implies that the Sex and Passenger Class agree with the prediction of Survival, namely "No". The red bars for Passenger Fare and relatives on board imply a disagreement with the prediction, and hence a positive correlation with survival.

The beauty of the Model Simulator is that it is interactive, so you can change all values at will, and immediately see the impact on predictions. Change the Sex from male to female, for example, and the probability of survival increases to roughly 50%. Then change the Passenger Class to first or second, and the probability of survival increases to over 90%.

By manipulating all the sliders and dropdown lists, you can quickly build some intuition for the model, even though it is built by Deep Learning.

The Model Simulator creates predictions by analyzing the behavior of the model in the neighborhood of a single data point (local correlation). To see which data columns have the greatest importance globally, notice the grey bars displayed under the column names (global correlation). Of these, the longest bar appears under Sex, followed by Passenger Class and Passenger Fare.

For more information, see the Model Simulator documentation.

Prescriptive Analytics

An obvious next question is: how should a passenger optimize his chance of survival on the Titanic?

Here too, Auto Model has an answer! At the bottom left of the simulator, there is a button labelled Optimize. Press this button, and a set of dialogs helps you to build a recipe. Since males on the Titanic are more at risk than females, let's find a survival strategy for males.

Press Optimize, and take the following steps:

1. Under Define Targets > Class to optimize for, choose "Yes". Press Next.
2. Under Define Constraints > Constant Attributes, press the + button, and select "Sex" equal to "Male". Press Next.
3. Under Optimization Parameters, press Run.
4. Press Finish.

The results are displayed immediately within the simulator, and the conclusion is striking. The male passenger with the best hope of survival on the Titanic is a 4 year-old boy, with only a few relatives, travelling in second class. His probability of survival is 91%. While class is definitely an issue on the Titanic, even a boy travelling third class has a good chance of survival, namely 68%, as you can see by modifying the value for Passenger Class from the dropdown list.

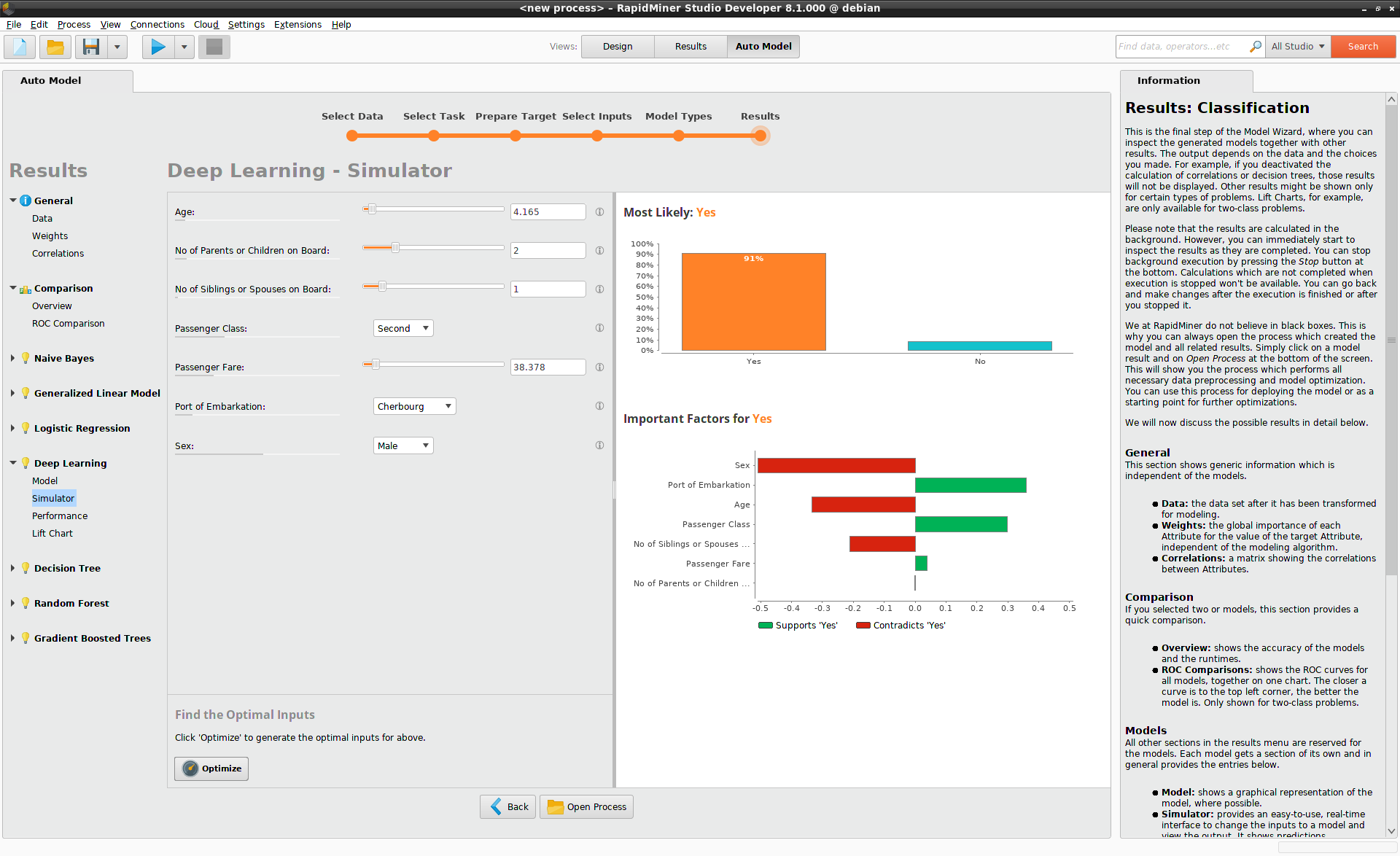
The Model Simulator makes it clear that the passengers on the Titanic adhered rather strictly to a philosophy of "women and children first" on the lifeboats. By moving the slider for Age, you can see that the probability of survival decreases continuously for older males. The age at which the probability of survival for male passengers dips below 50% is a function of class:

• Age 16 in third class
• Age 26 in second class
• Age 39 in first class

Strictly speaking, we haven't really answered the question of how a male passenger should improve his chance of survival. His age is given, and a more expensive ticket may be financially out of reach. But together the optimizer and the Model Simulator have given us a much better understanding of the Titanic data.

For more information, see the Prescriptive Analytics documentation.

No Black Boxes

Although Auto Model provides a lot of useful tools, you may want to see for yourself! Press Open Process at the bottom of the Model Simulator, and the process used to build the model is displayed in Altair AI Studio's Design view. You can run this process, you can modify this process, you can make any changes you like! Auto Model gives you the tools to solve your problem, with no black boxes.

Why do we stress this point? There are at least three reasons:

1. You would never put a model into production without first understanding it. You want to check how the model works, and prove to yourself that everything is correct.
2. New data scientists can learn best practices by examining the process.
3. Expert data scientists get a productivity boost, by using the Auto Model process as a starting point for their own models.